Question

24 POINTS!!!!!!!!!!!!!!

A semicircle is attached to the side of a rectangle as shown.

What is the best approximation for the area of this figure?

Use 3.14 to approximate pi.

The area is ________

Answer 1

Area of the figure = Area of rectangle + area of semi-circle

Area of rectangle = a * b = 6 * 2 = 12 m²

Area of the semi-circle = πr²/2 = 3.14 * (1.5)²/2
A = 3.53

Area of figure = 12 + 3.53 = 15.53 m²

In short, Your Final Answer would be: 15.53 m²

Hope this helps!

Answer 2

`15.5\ m^(2)`

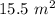
Explanation:

we know that

The area of the figure is equal to the area of a rectangle plus the area of semicircle

Step 1

Find the area of the rectangle

The area of the rectangle is equal to

`A=bh`

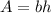
we have

`b=6\ m`

`h=2\ m`

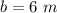
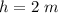
substitute

`A=6*2=12\ m^(2)`

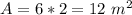
Step 2

Find the area of semicircle

The area of semicircle is equal to

`A=(1)/(2)\pi r^(2)`

we have

`r=3/2=1.5\ m`

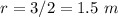
substitute

`A=(1)/(2)(3.14)(1.5^(2))=3.5\ m^(2)`

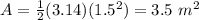
Step 3

Find the area of the figure

`12\ m^(2)+3.5\ m^(2)=15.5\ m^(2)`