see the attached figure to better understand the problem
we know that
An angle bisector divides the angle into two angles with equal measures
So
m∠CEA=
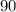 °
°
m∠AEB=m∠BEC=
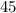 °
°
Statements
case 1) m∠CEA=
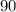 °
°
Is True
∠CEA is a right angle
case 2) m∠CEF = m∠CEA + m∠BEF
Is False
we know that
m∠CEF=
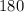 ° ---> is a straight angle
° ---> is a straight angle
and
m∠CEA + m∠BEF=
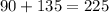 °
°
m∠CEF
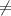 m∠CEA + m∠BEF
m∠CEA + m∠BEF
case 3) m∠CEB = 2(m∠CEA)
Is False
m∠CEB=
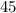 °
°
2(m∠CEA)=
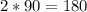 °
°
m∠CEB
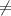 2(m∠CEA)
2(m∠CEA)
case 4) m∠BEF = 135°
Is True
m∠BEF=m∠BEA+m∠AEF
m∠BEA=
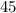 °
°
m∠AEF=
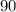 °
°
Substitute
m∠BEF=
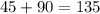 °
°
case 5) ∠CEF is a straight angle
Is True
m∠CEF=
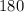 °
°
case 6) ∠AEF is a right angle
Is True
m∠AEF=
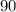 °
°
therefore
the answers are
m∠CEA=
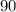 °
°
m∠BEF = 135°
∠CEF is a straight angle
∠AEF is a right angle