Question

If the smallest angle of rotation for a regular polygon is 18°, how many sides does polygon have? 10 12 20 24

Answer 1

Since the sum of the angles is 360°, we need to divide 360 with the number of sides that a polygon has.
360/18=20; this polygon has 20 sides.
Result:20

Answer 2

The polygon has 20 sides (Icosagon)

Explanation:

As the smallest angle of rotation for a regular polygon is 18°, so a 18° rotation yields the same figure.

According to the attachment, the side AB subtends an angle of 18° at the centre. That is why a 18° rotation generates the same figure.

According to the properties of regular polygon,

`OA=OB\ \ \Rightarrow m\angle OAB=m\angle OBA`

And

`m\angle OAC=m\angle OAB`

(as the radius of a regular polygon bisects the interior angle)

As in the triangle OAB,

`\Rightarrow m\angle AOB+m\angle OAB+m\angle OBA=180^(\circ)`

`\Rightarrow 18^(\circ)+2m\angle OAB=180^(\circ)`

`\Rightarrow m\angle OAB=81^(\circ)`

So,

`\Rightarrow m\angle CAB=2m\angle OAB=162^(\circ)`

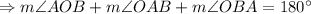
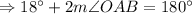
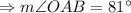
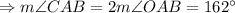
So, interior angle of polygon is 162°

We know that, the interior angle of regular polygon with n side is,

`=((n-2)180)/(n)`

Hence,

`\Rightarrow ((n-2)180)/(n)=162`

`\Rightarrow (n-2)180=162n`

`\Rightarrow 180n-360=162n`

`\Rightarrow 180n-162n=360`

`\Rightarrow 18n=360`

`\Rightarrow n=20`

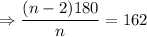
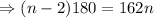
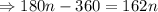
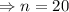
Therefore, the polygon has 20 sides (Icosagon)