Answer:
The polygon has 20 sides (Icosagon)
Explanation:
As the smallest angle of rotation for a regular polygon is 18°, so a 18° rotation yields the same figure.
According to the attachment, the side AB subtends an angle of 18° at the centre. That is why a 18° rotation generates the same figure.
According to the properties of regular polygon,
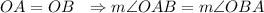
And
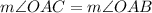
(as the radius of a regular polygon bisects the interior angle)
As in the triangle OAB,
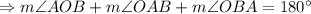
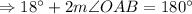
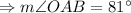
So,
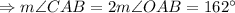
So, interior angle of polygon is 162°
We know that, the interior angle of regular polygon with n side is,
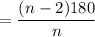
Hence,
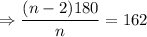
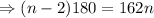
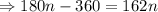
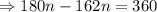
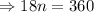
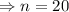
Therefore, the polygon has 20 sides (Icosagon)