Question

What is the 32nd term of the arithmetic sequence where a1 = 14 and a13 = −58?

−178
−172
−166
−160

I somehow got -704 can someone help me please.

Answer 1

a1 = 14
a13 = -58

a13 = a1 + 12d
-58 = 14 + 12d
12d = -58 -14
12d = -72
d = -72/12 = -6

a32 = a1 + 31d = 14 - 31*6 = 14 - 186 = -172

Answer 2

Answer: The correct option is (B) -172.

Step-by-step explanation: We are given to find the 32nd term of the arithmetic sequence where the 1st term and 13th term are

`a_1=14,~~~a_(13)=-58.`

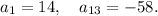
We know that

the n-th term of an arithmetic sequence with first term
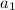`a_1` and common difference
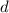`d` is given by

`a_n=a_1+(n-1)d.`

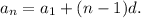
According to the given information, we have

`a_1=14,`

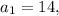
and

`a_(13)=-58\\\\\Rightarrow a_1+(13-1)d=-58\\\\\Rightarrow 14+12d=-58\\\\\Rightarrow 12d=-58-14\\\\\Rightarrow 12d=-72\\\\\Rightarrow d=-6.`

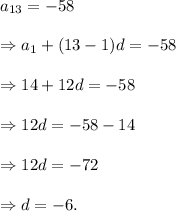
Therefore, the 32nd term will be

`a_(32)=a_1+(32-1)d=14+31*(-6)=14-186=-172.`

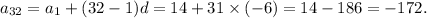
Thus, the 32nd term is -172.

Option (B) is correct.