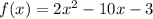What are the zeros of the quadratic function f(x)=2x^2-10x-3

Question

asked Mar 15, 2018 107k views

2 Answers

Jon Rubins · Answer 1 · 2018-03-19T08:17:13+0000

The zeros of the quadratic function
f(x)=2x^2-10x-3 are:

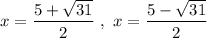
$x=(5+√(31))/(2)\ ,\ x=(5-√(31))/(2)$

Zeros of a function are the possible x values of the function for which the function is equal to zero.

i.e. all those x for which f(x)=0

We are given a function f(x) by:

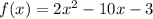
f(x)=2x^2-10x-3

Now, f(x)=0

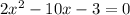
2x^2-10x-3=0

We know that the solution of the quadratic equation of the type:

ax^2+bx+c=0 is given by:

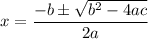
$x=(-b\pm √(b^2-4ac))/(2a)$

Here we have:

a=2, b= -10 and c= -3

Hence, the solution is:

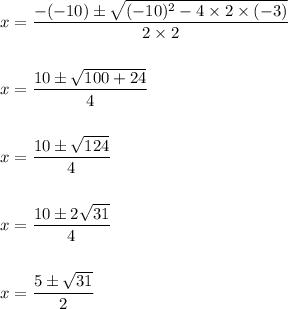
$x=(-(-10)\pm √((-10)^2-4* 2* (-3)))/(2* 2)\\\\\\x=(10\pm √(100+24))/(4)\\\\\\x=(10\pm √(124))/(4)\\\\\\x=(10\pm 2√(31))/(4)\\\\\\x=(5\pm √(31))/(2)$

Hence,

x=(5+√(31))/(2) and
x=(5-√(31))/(2)