Answer:
He invested
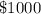 in first account and
in first account and
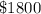 in the second account.
in the second account.
Step-by-step explanation:
Let the man invest
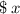 in the first account.
in the first account.
It is given that he gets a 2% interest on the first amount.
Let
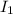 represents the interest received after 1 year.
represents the interest received after 1 year.
We know that
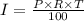
Here,
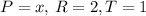
So,
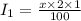
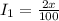
It is given that he invest
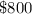 more at 4% interest on the second amount.
more at 4% interest on the second amount.
Let
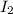 represents the interest received after 1 year.
represents the interest received after 1 year.
We know that
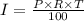
In that case,

So,
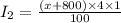
I_{2}=\frac{4x+3200}{100}
Also, it is given that the total interest he earned is

So, we have
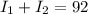
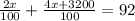
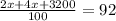
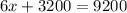
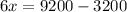

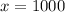
Hence, he invested
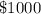 in first account and
in first account and
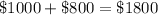 in the second account.
in the second account.