Answer:
d) 28 degrees
Explanation:
Be,
a = MN = 20
b = NO = 15
c = MO = 18
A = angle opposite side "a"
B = angle opposite side "b"
C = angle opposite side "c"
By the law of cosines, we know that,
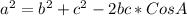
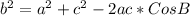
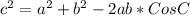
Isolating "A" from the first equation we can clamp the angle opposite to the side "a", as follows
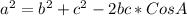
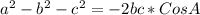
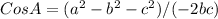
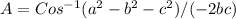
Replace the values and calculate the value of angle "A", like this
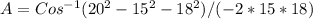
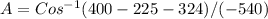
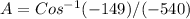
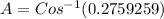
A = 73.98 ~ 74 degrees
Now calculate the value of angle B in a similar way,
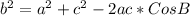
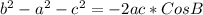
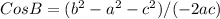
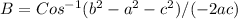
Replace the values and calculate the value of angle "B", like this
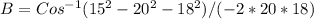
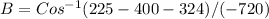
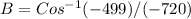
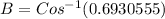
B = 46.13 ~ 46 degrees
The sum of the angles of a triangle is 180 degrees, that is,
A + B + C = 180 degrees
Isolating C,
C = 180 - A - B
C = 180 - 74 - 46
C = 60
Being A = 74, B = 46, C = 60, then the approximate difference between the major and minor angle measures is,
Difference = A - C
Difference = 74 - 46
Difference = 28 degrees
Hope this helps!