Question

In triangle MNO, MN=20, NO=15, and MO=18. What is the approximate difference between the largest and smallest angle measures?

a) 2 degrees
b) 5 degrees
c) 14 degrees
d) 28 degrees

Answer 1

a) 2 degrees is the answer

Answer 2

d) 28 degrees

Explanation:

Be,

a = MN = 20

b = NO = 15

c = MO = 18

A = angle opposite side "a"

B = angle opposite side "b"

C = angle opposite side "c"

By the law of cosines, we know that,

`a^(2)=b^(2)+c^(2)-2bc*CosA`

`b^(2)=a^(2)+c^(2)-2ac*CosB`

`c^(2)=a^(2)+b^(2)-2ab*CosC`

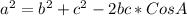
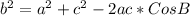
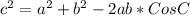
Isolating "A" from the first equation we can clamp the angle opposite to the side "a", as follows

`a^(2)=b^(2)+c^(2)-2bc*CosA`

`a^(2)-b^(2)-c^(2)=-2bc*CosA`

`CosA=(a^(2)-b^(2)-c^(2)) / (-2bc)`

`A=Cos^(-1)(a^(2)-b^(2)-c^(2)) / (-2bc)`

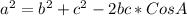
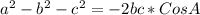
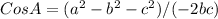
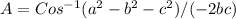
Replace the values ​​and calculate the value of angle "A", like this

`A=Cos^(-1)(20^(2)-15^(2)-18^(2)) / (-2*15*18)`

`A=Cos^(-1)(400-225-324) / (-540)`

`A=Cos^(-1)(-149) / (-540)`

`A=Cos^(-1)(0.2759259)`

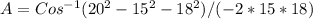
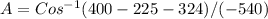
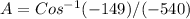
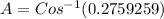
A = 73.98 ~ 74 degrees

Now calculate the value of angle B in a similar way,

`b^(2)=a^(2)+c^(2)-2ac*CosB`

`b^(2)-a^(2)-c^(2)=-2ac*CosB`

`CosB=(b^(2)-a^(2)-c^(2)) / (-2ac)`

`B=Cos^(-1)(b^(2)-a^(2)-c^(2)) / (-2ac)`

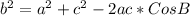
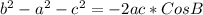
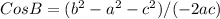
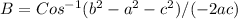
Replace the values ​​and calculate the value of angle "B", like this

`B=Cos^(-1)(15^(2)-20^(2)-18^(2)) / (-2*20*18)`

`B=Cos^(-1)(225-400-324) / (-720)`

`B=Cos^(-1)(-499) / (-720)`

`B=Cos^(-1)(0.6930555)`

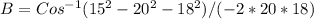
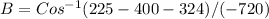
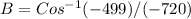
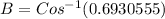
B = 46.13 ~ 46 degrees

The sum of the angles of a triangle is 180 degrees, that is,

A + B + C = 180 degrees

Isolating C,

C = 180 - A - B

C = 180 - 74 - 46

C = 60

Being A = 74, B = 46, C = 60, then the approximate difference between the major and minor angle measures is,

Difference = A - C

Difference = 74 - 46

Difference = 28 degrees

Hope this helps!