Answer:
The change in volume of water in the tank after 35 second is approximately 687223.393 cubic centimeters.
Explanation:
Geometrically speaking, the volume of the cylindrical tank (
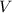 ), measured in cubic centimeters, is determined by the following formula:
), measured in cubic centimeters, is determined by the following formula:
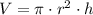 (1)
(1)
Where:
 - Radius, measured in centimeters.
- Radius, measured in centimeters.
 - Height, measured in centimeters.
- Height, measured in centimeters.
By Differential Calculus, we obtain a formula of the rate of change of the volume of the cylinder (
 ), measured in cubic centimeters per seconds:
), measured in cubic centimeters per seconds:
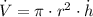 (2)
(2)
Where
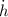 is the rate of change of the water level, measured in centimeters per second.
is the rate of change of the water level, measured in centimeters per second.
Given that the rate of change of the water level is constant, then the rate of change of the volume of the cylinder is also constant. Hence, the change in the volume of the cylinder (
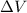 ), measured in cubic centimeters, is:
), measured in cubic centimeters, is:
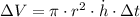 (3)
(3)
If we know that
 ,
,
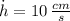 and
and
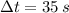 , then the change in the volume of water in the tank is:
, then the change in the volume of water in the tank is:
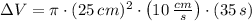
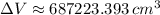
The change in volume of water in the tank after 35 second is approximately 687223.393 cubic centimeters.