Question

The radius of the base of a cylindrical tank is 25cm,if the water level rises 10cm/s .Calculate the change in volume of water in the tank after 35seconds. Can you help me with this question?

Answer 1

The change in volume of water in the tank after 35 second is approximately 687223.393 cubic centimeters.

Explanation:

Geometrically speaking, the volume of the cylindrical tank (
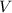`V`), measured in cubic centimeters, is determined by the following formula:

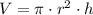`V = \pi\cdot r^(2)\cdot h` (1)

Where:

`r` - Radius, measured in centimeters.

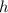`h` - Height, measured in centimeters.

By Differential Calculus, we obtain a formula of the rate of change of the volume of the cylinder (
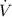`\dot V`), measured in cubic centimeters per seconds:

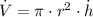`\dot V = \pi\cdot r^(2)\cdot \dot h` (2)

Where
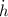`\dot h` is the rate of change of the water level, measured in centimeters per second.

Given that the rate of change of the water level is constant, then the rate of change of the volume of the cylinder is also constant. Hence, the change in the volume of the cylinder (
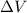`\Delta V`), measured in cubic centimeters, is:

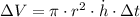`\Delta V = \pi\cdot r^(2)\cdot \dot h \cdot \Delta t` (3)

If we know that
`r = 25\,cm`,
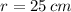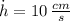`\dot h = 10\,(cm)/(s)` and
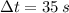`\Delta t = 35\,s`, then the change in the volume of water in the tank is:

`\Delta V = \pi\cdot (25\,cm)^(2)\cdot \left(10\,(cm)/(s) \right)\cdot (35\,s)`

`\Delta V \approx 687223.393\,cm^(3)`

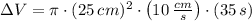
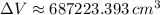
The change in volume of water in the tank after 35 second is approximately 687223.393 cubic centimeters.