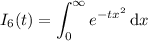Question

Using laplace theorem find the answer

Answer 1

Here's the general approach.

For the first integral, assume
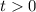
`t>0`. I'm also interpreting it to say


`I_1=\displaystyle\int_0^\infty\sin(tx^2)\,\mathrm dx`

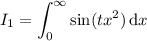
(otherwise the integral simply diverges).

Writing
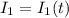
`I_1=I_1(t)`, take the Laplace transform to get


`\mathcal L_s\{I_1(t)\}=\displaystyle\int_0^\infty\left(\int_0^\infty\sin(tx^2)\,\mathrm dx\right)e^(-st)\,\mathrm dt`

`\mathcal L_s\{I_1(t)\}=\displaystyle\int_0^\infty\left(\underbrace{\int_0^\infty \sin(tx^2)e^(-st)}_{\mathcal L_s\{\sin(tx^2)\}}\,\mathrm dt\right)\,\mathrm dx`

`\mathcal L_s\{I_1(t)\}=\displaystyle\int_0^\infty(x^2)/(s^2+x^4)\,\mathrm dx`

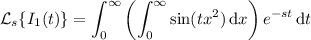
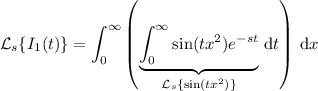
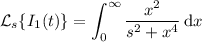
which is an elementary integral that can be computed by decomposing into partial fractions, or by employing a proper trigonometric substitution. I leave that calculation to you; you should end up with


`\mathcal L_s\{I_1(t)\}=\frac\pi{2√(2s)}`

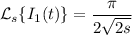
and taking the inverse Laplace transform yields the answer,


`I_1(t)=\mathcal L_t^(-1)\left\{\frac\pi{2√(2s)}\right\}=(\sqrt\pi)/(2√(2t))`

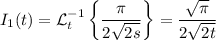
Hopefully that should give you a decent idea of how this method works.

For the remaining integrals, you will need to introduce a parameter before proceeding. Here's what you can try:


`I_2(t)=\displaystyle\int_0^\infty\frac{\sin(tx)}x\,\mathrm dx`

`I_3(t)=\displaystyle\int_0^\infty\frac{1-\cos(tx)}x\,\mathrm dx`

`I_4(t)=\displaystyle\int_0^\infty\frac{\sin^2(tx)}x\,\mathrm dx`

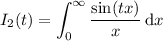
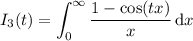
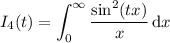
For the fifth integral, you can make the observation that the given integrand already resembles the Laplace transform of
`\frac{\sin t}t`:


`\underbrace{\mathcal L_s\left\{\frac{\sin t}t\right\}}_(Y(s))=\displaystyle\int_0^\infty e^(-st)\underbrace{\frac{\sin t}t}_(y(t))\,\mathrm dt\implies \int_0^\infty e^(-4t)\frac{\sin t}t\,\mathrm dt=Y(4)`

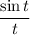
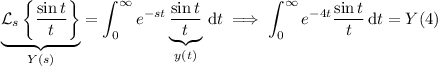
Finally, for the last integral, you can use


`I_6(t)=\displaystyle\int_0^\infty e^(-tx^2)\,\mathrm dx`