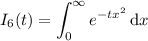Here's the general approach.
For the first integral, assume

. I'm also interpreting it to say
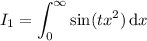
(otherwise the integral simply diverges).
Writing
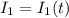
, take the Laplace transform to get

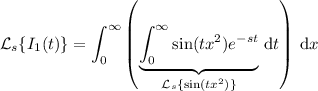
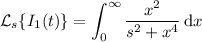
which is an elementary integral that can be computed by decomposing into partial fractions, or by employing a proper trigonometric substitution. I leave that calculation to you; you should end up with
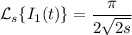
and taking the inverse Laplace transform yields the answer,

Hopefully that should give you a decent idea of how this method works.
For the remaining integrals, you will need to introduce a parameter before proceeding. Here's what you can try:
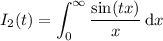
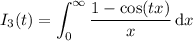
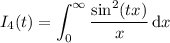
For the fifth integral, you can make the observation that the given integrand already resembles the Laplace transform of

:
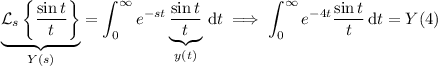
Finally, for the last integral, you can use