Let
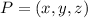
be an arbitrary point on the surface. The distance between
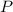
and the given point

is given by the function
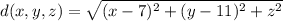
Note that

and
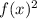
attain their extrema, if they have any, at the same values of

. This allows us to consider the modified distance function,
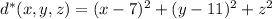
So now you're minimizing
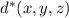
subject to the constraint

. This is a perfect candidate for applying the method of Lagrange multipliers.
The Lagrangian in this case would be

which has partial derivatives

Setting all four equation equal to 0, you find from the third equation that either
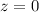
or
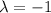
. In the first case, you arrive at a possible critical point of
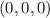
. In the second, plugging
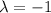
into the first two equations gives

and plugging these into the last equation gives
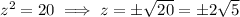
So you have three potential points to check:
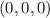
,
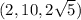
, and
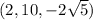
. Evaluating either distance function (I use
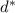
), you find that
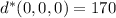
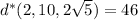
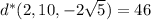
So the two points on the surface

closest to the point

are
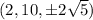
.