Answer:
s measures 33° and t measures 57°.
Explanation:
Since the two angles s and t are complementary, this implies that:
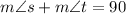
We are given that t is 9 less than twice s. Hence:
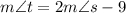
We can substitute this into the first equation:
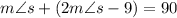
Solve for s. Combine like terms:

Adding 9 to both sides yields:
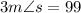
And dividing both sides by 3 gives us that:
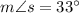
Returning to our second equation, we have:
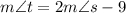
So:
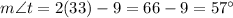
So, s measures 33° and t measures 57°.