Answer:
The average rate of change of the height
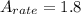
Explanation:
The average rate of change of a function is given by:
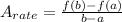
Where:
f(x) is the funtion, in our case
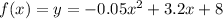
f(b) is the function evaluated in b, when b = 20
f(a) is the funtion evaluated in a, when a = 8
Let's find f(a) and f(b):
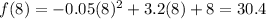
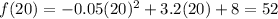
Therefore, using the average rate of change equation.
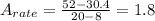
I hope it helps you!