Question

The path of a baseball thrown at an angle of 40 degrees can be modeled by y=-0.05x^2+3.2x+8y=−0.05x 2 +3.2x+8 where x is the horizontal distance in feet from the release point and y is the corresponding height, in feet. Calculate the average rate of change of the height over the interval 8\le x\le208≤x≤20.

Answer 1

The average rate of change of the height
`A_(rate)=1.8`

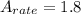
Explanation:

The average rate of change of a function is given by:

`A_(rate)=(f(b)-f(a))/(b-a)`

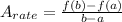
Where:

f(x) is the funtion, in our case
`f(x) = y = -0.05x^(2)+3.2x+8`

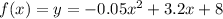
f(b) is the function evaluated in b, when b = 20

f(a) is the funtion evaluated in a, when a = 8

Let's find f(a) and f(b):

`f(8) = -0.05(8)^(2)+3.2(8)+8=30.4`

`f(20) = -0.05(20)^(2)+3.2(20)+8=52`

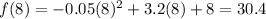
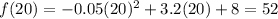
Therefore, using the average rate of change equation.

`A_(rate)=(52-30.4)/(20-8)=1.8`

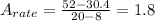
I hope it helps you!