Answer:
The energy released during the change is
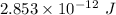 .
.
Step-by-step explanation:
Given that,
Total mass
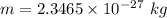
After change , the mass of resulting materials
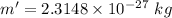
Using the Einstein's mass energy equation
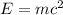
The energy released during the change is given by
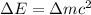
Where,
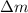 is the change of mass in the process
is the change of mass in the process
c = speed of light
The change in mass
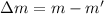
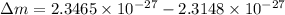
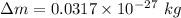
We substitute the value into the formula
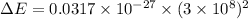
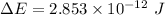
Hence, The energy released during the change is
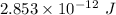 .
.