Question

Triangle K L J is cut by line segment N O. Line segment N O goes from side L K to side L J. The length of L N is (x minus 3) inches, the length of N K is (x + 2) inches, the length of L O is (x minus 4) inches, and the length of O J is x inches. Which value of x would make Line segment N O is parallel to line segment K J? 1 6 8 10

Answer 1

Option C- 8

Step-by-step explanation:

Plug it in- Hope this helps :)

Answer 2

Answer: x= 8

Step-by-step explanation:

According to the converse of basic proportionality theorem,

If in ΔABC , DE is a line drawn from AB to AC such that
`(AD)/(DB)=(AE)/(EB)`

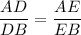
then, DE is parallel to the third side BC.

Applying converse of basic proportionality theorem, to get NO parallel to KJ, we must have

`(LO)/(OJ)=(LN)/(NK)\\\\\Rightarrow (x-4)/(x)=(x-3)/(x+2)\\\\\Rightarrow\ (x-4)(x+2)=x(x-3)\\\\\Rightarrow\ x^2-2x-8=x^2-3x\\\\\Rightarrow\ -2x+3x=8\\\\\Rightarrow\ x=8`

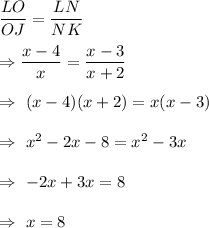
Hence, the value of x should be 8, so that Line segment N O is parallel to line segment K J.