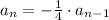Answer:

Explanation:
The recursive formula for the geometric sequence is given by:
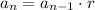
where,
r is the common ratio terms.
Given the sequence:
-16, 4, -1, ...
This is a geometric sequence.
Here,
 and
and
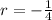
Since,

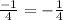 ans so on .....
ans so on .....
Substitute the given values we have;
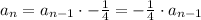
⇒
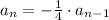
Therefore, the recursive formula for the following geometric sequence is,