Question

The length of ​ AB¯¯¯¯¯ ​ is 9 centimeters. A dilation with a scale factor of 2 is applied to ​ AB¯¯¯¯¯ ​ . What is the length of the image of ​ AB¯¯¯¯¯ ​ after the dilation is applied? Enter your answer in the box

Answer 1

Scale factor(k) defined as:

`k = \frac{\text{Dilated image}}{\text{original image}}`

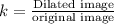
As per the statement:

The original length of AB is 9 centimeters.

A dilation with a scale factor of 2 is applied to ​AB.

⇒k = 2

We have to find the length of the image of ​ AB after the dilation is applied.

Using definition of scale factor:

`k = \frac{\text{Length of Dilated image AB}}{\text{Length of original image AB}}`

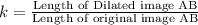
Substitute the given values we have;

`2= \frac{\text{Length of Dilated image AB}}{9}`

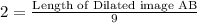
Multiply both sides by 9 we have;

`18 = \text{Length of image of AB}`

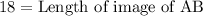
or

`\text{Length of image of AB} =18`

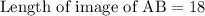
therefore, the length of the image of ​ AB after the dilation is applied. is, 18