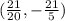Question

Solve the system by substitution.
y = -4x
23 - 5y = 44

Answer 1

Step-by-step explanation

• Given the system of equations.

`\begin{cases} y = - 4x \\ 23 - 5y = 44 \end{cases}`

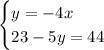
• Substitute y = -4x in the second equation.

`23 - 5( - 4x) = 44 \\ 23 + 20x = 44 \\ 20x = 44 - 23 \\ 20x = 21 \\ x = (21)/(20)`

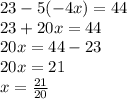
• Substitute the value of x in any given equations. I will substitute the value of x in the first equation.

`y = - 4x \Longrightarrow y = - 4( (21)/(20) ) \\ y = \cancel{ - 4}( \frac{21}{ \cancel{20}} ) \Longrightarrow y = - (21)/(5) \\ y = - (21)/(5)`

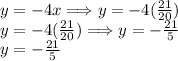
• Answer Check by substituting both values in two equations.

First Equation

`y = - 4x \Longrightarrow - (21)/(5) = - 4( (21)/(20) ) \\ - (21)/(5) = \cancel{ - 4}( \frac{21}{ \cancel{20}} ) \\ - (21)/(5) = - (21)/(5) \: \: \: \checkmark`

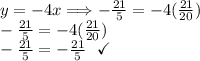
Second Equation

`23 - 5y = 44 \\ 23 - 5( - (21)/(5) ) = 44 \\23 - \cancel{5}( - \frac{21}{ \cancel{5}} ) = 44 \\ 23 + 21 = 44 \\ 44 = 44 \: \: \: \: \checkmark`

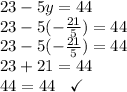
Both equations are true for the value of x and value of y.

Answer

`\begin{cases} x = (21)/(20) \\ y = - (21)/(5) \end{cases}`

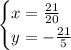
Coordinate Point form

`( (21)/(20) , - (21)/(5) )`