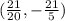Step-by-step explanation
- Given the system of equations.
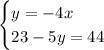
- Substitute y = -4x in the second equation.
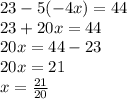
- Substitute the value of x in any given equations. I will substitute the value of x in the first equation.
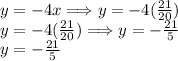
- Answer Check by substituting both values in two equations.
First Equation
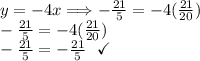
Second Equation
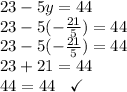
Both equations are true for the value of x and value of y.
Answer
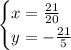
Coordinate Point form