Answer:
The equation is
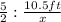 ; The value of x is 4.2ft.
; The value of x is 4.2ft.
Explanation:
A ratio is like a constant that remains between two values, and we can use it to find whatever others that keep the same constant relation between them.
Hank wants a dog run that keeps a constant relation between length to the width. That is, the length must be 2.5 times to the width (
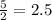 ).
).
So, knowing that ratio or constant, we can represent it as follows:
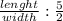 [ 1 ]
[ 1 ]
But, it also could be expressed as the relation between the width to the length:
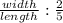 [ 2 ]
[ 2 ]
He wants a lenght of 10.5ft for building a dog run for his dog, and that this new value must keep the ratio just explained [ 1 ] to the width expected.
So, the equation is:
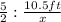
And we have to find the value for x that solve this equation.
However, we can use an easier way to represent this using the equation [ 2 ] for solving x :

That is, the width must be 4.2ft to keep the ratio length to the width 5:2 ( or the ratio width to the length 2:5).
To check this answer:

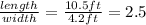 .
.
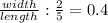
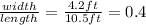 .
.