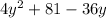Answer:
The polynomial whose factored form is
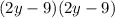
is
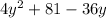
Explanation:
Given : Factored form of a polynomial as
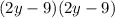
We have to find the polynomial whose factored form is
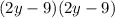
Consider the given expression
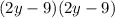
We have,
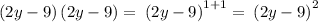
Thus, Applying algebraic identity,
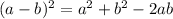 , we have,
, we have,
a = 2y and b = 9
Thus,
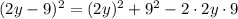
Simplify, we have,
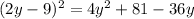
Thus, The polynomial whose factored form is
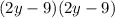
is