Answer:
2 was added to each side
Explanation:
Given that a rectangle when changed sides, the area became 60 greater than the original
The equation given is
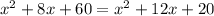
From the above equation we can see that the original area was
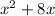
and it changed to

Original rectangle dimensions= factors of area terms = x , x+8
New rectangle dimensions = factors of

=x+2, x+10
Thus we have both length and width increased by 2 units.