Question

Use the explicit or recursive formulas for the geometric sequence 45,135,140,1215,3645... To the sum of the first 9 terms of the sequence

Answer 1

`S_9 = 442845`

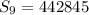
Explanation:

Given

`Sequence: 45,135,405,1215,3645`

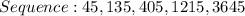
Required:

The sum of the first 9 terms

We'll solve this question using the explicit formula:

Because it is a geometric sequence, we first calculate the common ratio (r).

`r = (T_n)/(T_(n-1))`

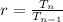
Let n = 2;

So, we have:

`r = (T_2)/(T_(2-1))`

`r = (T_2)/(T_1)`

`T_2 = 135; T_1 = 45`

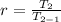
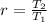
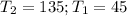
So, we have:

`r = (135)/(45)`

`r = 3`

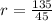
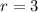
Explicitly, the sum of n terms of a geometric sequence is:

`S_n = (a(r^n - 1))/(r - 1)`

`a = T_1 = 45`

`r = 3`

`n = 9`

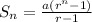
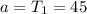
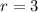
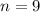
The formula becomes:

`S_n = (a(r^n - 1))/(r - 1)`

`S_9 = (45* (3^9 - 1))/(3 - 1)`

`S_9 = (45* (3^9 - 1))/(2)`

`S_9 = (45* (19683 - 1))/(2)`

`S_9 = (45* (19682))/(2)`

`S_9 = 45* 9841`

`S_9 = 442845`

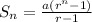
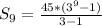
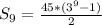
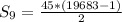
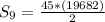
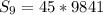
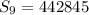
Hence, the sum of the first 9 terms is 442845