Answer:
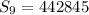
Explanation:
Given
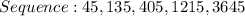
Required:
The sum of the first 9 terms
We'll solve this question using the explicit formula:
Because it is a geometric sequence, we first calculate the common ratio (r).

Let n = 2;
So, we have:

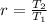
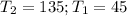
So, we have:
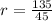
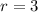
Explicitly, the sum of n terms of a geometric sequence is:
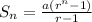
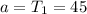
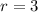
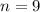
The formula becomes:
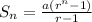
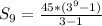
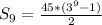
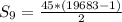

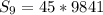
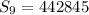
Hence, the sum of the first 9 terms is 442845