Answer: The required dimensions of the rectangle are 15 inches and 8 inches.
Step-by-step explanation: Given that the The width of a rectangle is 7 inches less than its length and the area of the rectangle is 120 square inches.
We are to find the dimensions of the rectangle.
Let, 'l' and 'b' represents the length and breadth of the rectangle.
So, b = l - 7.
Now, the AREA of the rectangle will be
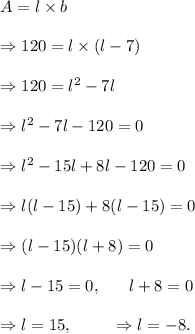
Since the length cannot be negative, so l = 15 inches.
Therefore, the breadth of the rectangle will be (15 - 8) = 7 inches.
Thus, the required dimensions of the rectangle are 15 inches and 8 inches.