We're differentiating implicitly which means we're not going to find an explicit function y(x) before differentiating.
Simply power rule each term and don't forget to chain on the y. Since it's not x, we end up with this extra derivative thing y'.
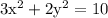

Plug in x and y,
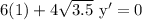
and solve for y',
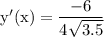
Hope that helps.