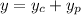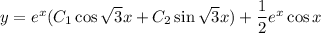Question

D^2y/dx^2 - 2 dy/dx + 4y = e^x*cosx

Answer 1

First, the characteristic solution to the homogeneous part:


`(\mathrm d^2y)/(\mathrm dx^2)-2(\mathrm dy)/(\mathrm dx)+4y=0`

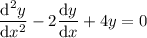
has characteristic equation


`r^2-2r+4=0`

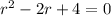
with roots
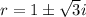
`r=1\pm\sqrt3i`. So the characteristic solution has the form


`y_c=e^x(C_1\cos\sqrt3x+C_2\sin\sqrt3x)`

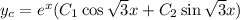
Now for the nonhomogeneous part. Using the method of undetermined coefficients, we can try a particular solution of the form


`y_p=e^x(a\cos x+b\sin x)`

which has derivatives


`(\mathrm dy_p)/(\mathrm dx)=e^x((a+b)\cos x+(-a+b)\sin x)`

`(\mathrm d^2y_p)/(\mathrm dx^2)=2e^x(b\cos x-a\sin x)`

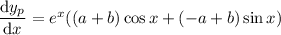
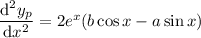
Substituting
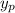
`y_p` and its derivatives into the equation gives


`2e^x(b\cos x-a\sin x)-2e^x((a+b)\cos x+(-a+b)\sin x)+4e^x(a\cos x+b\sin x)=e^x\cos x`

`2e^x(a\cos x+b\sin x)=e^x\cos x`

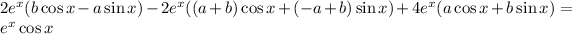
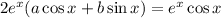
which means


`\begin{cases}2a=1\\2b=0\end{cases}\implies a=\frac12,b=0`

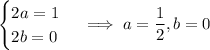
so that the particular solution must be


`y_p=\frac12e^x\cos x`

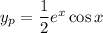
Now the general solution will be


`y=y_c+y_p`

`y=e^x(C_1\cos\sqrt3x+C_2\sin\sqrt3x)+\frac12e^x\cos x`