There are 26 integers in the set
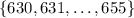
. If the wavelength of light is uniformly distributed, then the probability that it has a wavelength of any one of these integers is

, so the distribution of wavelengths has probability mass function

The mean (expected value) is given by
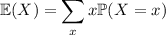
and the variance by
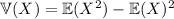
First, the mean:

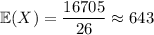
(rounded up from an exact value of 642.5)
Now for the variance:


Meanwhile,
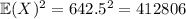
, which gives a total variance of
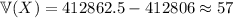
(rounded up from 56.5)