Question

Assume that the wavelengths of photosynthetically active radiations (PAR) are uniformly distributed at integer nanometers in the red spectrum from 630 to 655 nm. What is the mean and variance of the wavelength distribution for this radiation

Answer 1

There are 26 integers in the set
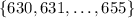
`\{630,631,\ldots,655\}`. If the wavelength of light is uniformly distributed, then the probability that it has a wavelength of any one of these integers is
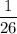
`\frac1{26}`, so the distribution of wavelengths has probability mass function


`\mathbb P(X=x)=\begin{cases}\frac1{26}&\text{for }630\le x\le655,x\in\mathbb Z\\\\0&\text{otherwise}\end{cases}`

The mean (expected value) is given by


`\mathbb E(X)=\displaystyle\sum_xx\mathbb P(X=x)`

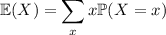
and the variance by


`\mathbb V(X)=\mathbb E(X^2)-\mathbb E(X)^2`

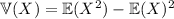
First, the mean:


`\mathbb E(X)=\displaystyle\sum_(x=630)^(655)x\mathbb P(X=x)=\frac1{26}\sum_(x=630)^(655)x`

`\mathbb E(X)=(16705)/(26)\approx643`

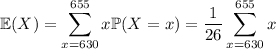
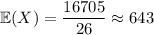
(rounded up from an exact value of 642.5)

Now for the variance:


`\mathbb E(X^2)=\displaystyle\sum_xx^2\mathbb P(X=x)=\frac1{26}\sum_(x=630)^(655)x^2`

`\mathbb E(X^2)=412862.5`

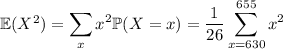
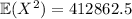
Meanwhile,
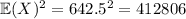
`\mathbb E(X)^2=642.5^2=412806`, which gives a total variance of


`\mathbb V(X)=412862.5-412806\approx57`

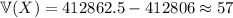
(rounded up from 56.5)