Answer:
The tension in the string is 276 N.
Step-by-step explanation:
It is given that,
Mass of the ball, m = 1.5 kg
Length of the meter stick, r = 0.52 m
Velocity of the ball, v = 9.78 m/s
The tension acting in the string is balanced by the centripetal force acting on it. Its formula is given by :
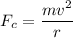

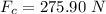
or
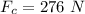
So, the tension in the string is 276 N. Hence, this is the required solution.