Question

Find the potential real zeros (roots) of the following equation. f(x) = 4x5 - 16x4 + 17x3 - 19x2 + 13x - 3 = 0

Answer 1

use the rational roots theorem
factors of 3 are 1, 3 and factors of 4 are 1,2 and 4

so potential roots are +/- ( 1/3 , 3, 1/2, 1/4 . 3/4)

Answer 2

The potential real zeros are
`\pm 1,\pm 3, \pm (1)/(2),\pm (3)/(2), \pm (1)/(4), \pm (3)/(4)`.

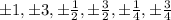Explanation:

The given polynomial is

`f(x)=4x^5-16x^4+17x^3-19x^2+13x-3=0`

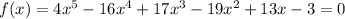
According to the rational root theorem, all the potential real zeros are in the form of

`r=\pm (p)/(q)`

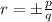
Where, p is the factor of constant and q is the factor of leading coefficient.

The constant term is -3 and leading coefficient is 4.

Factors of -3 are ±1, ±3.

Factors of 4 are ±1, ±2, ±4.

The potential real zeros are

`\pm 1,\pm 3, \pm (1)/(2),\pm (3)/(2), \pm (1)/(4), \pm (3)/(4)`

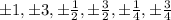
Therefore potential real zeros are
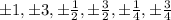`\pm 1,\pm 3, \pm (1)/(2),\pm (3)/(2), \pm (1)/(4), \pm (3)/(4)`.