Answer:
We conclude that
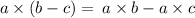
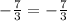
L.H.S = R.H.S
Explanation:
Given the property expression
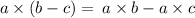
Given that:
Determining the LEFT-HAND SIDE
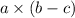
substituting a= -3/5, b= 5/9 and c= -10/3
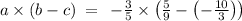
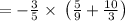
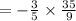
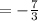
Determining the RIGHT-HAND SIDE
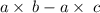
substituting a= -3/5, b= 5/9 and c= -10/3
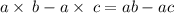
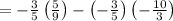
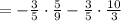
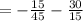
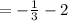
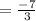
Apply the fraction rule:
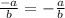
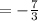
Therefore, we conclude that
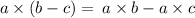
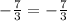
L.H.S = R.H.S