Answer:
1.
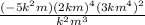 = -720
= -720
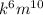
2.
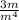 =
=
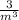 (or 3
(or 3
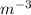 )
)
Explanation:
1. The given expression is:
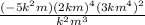
With respect to the principle of exponential, we have;
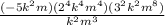 =
=
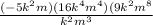
Applying the law of indices,
=
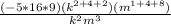
=
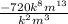
= -720
 x
x
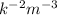
= -720
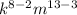
= -720
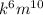
2.
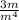
divide the numerator and denominator with common factor m,
=
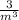
This can not be simplified further since there are no more common factors, so that;
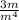 =
=
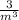 (or 3
(or 3
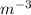 )
)