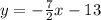Question

Find an equation for the perpendicular bisector of the line segment whose endpoints

(5,-4) and (-9, -8).
are

Answer 1

The equation for the perpendicular bisector of the line segment will be:

`y=-(7)/(2)x-13`

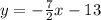
Explanation:

Given the endpoints of the line segments

• (5,-4)

• (-9, -8)

Determining the slope between (5,-4) and (-9, -8)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(5,\:-4\right),\:\left(x_2,\:y_2\right)=\left(-9,\:-8\right)`

`m=(-8-\left(-4\right))/(-9-5)`

`m=(2)/(7)`

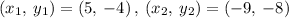
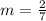
We know that a line perpendicular to another line contains a slope that is the negative reciprocal of the slope of the other line, such as:

slope = m = 2/7

Thus, the slope of the the new perpendicular line = – 1/m = (-1)/(2/7)= -7/2

Next, determining the mid-point between (5,-4) and (-9, -8)

`\mathrm{Midpoint\:of\:}\left(x_1,\:y_1\right),\:\left(x_2,\:y_2\right):\quad \left((x_2+x_1)/(2),\:\:(y_2+y_1)/(2)\right)`

`\left(x_1,\:y_1\right)=\left(5,\:-4\right),\:\left(x_2,\:y_2\right)=\left(-9,\:-8\right)`

`=\left((-9+5)/(2),\:(-8-4)/(2)\right)`

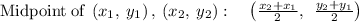
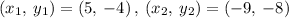
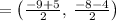
Refine

`=\left(-2,\:-6\right)`

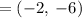
We know that the point-slope form of equation of line is

`y-y_1=m\left(x-x_1\right)`

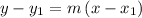
where

• m is the slope of the line

• (x₁, y₁) is the point

substituting the slope of the perpendicular line -7/2 and the point (-2, -6)

`y-y_1=m\left(x-x_1\right)`

`y-\left(-6\right)=-(7)/(2)\left(x-\left(-2\right)\right)`

`y+6=-(7)/(2)\left(x+2\right)`

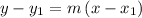
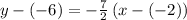
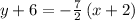
Subtract 6 from both sides

`y+6-6=-(7)/(2)\left(x+2\right)-6`

`y=-(7)/(2)x-13`

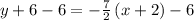
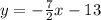
Therefore, the equation for the perpendicular bisector of the line segment will be:

`y=-(7)/(2)x-13`