Question

Find the zeroes of 6x^4+x^3+2x^2-4x+1

Answer 1

By the rational root theorem, you have the following candidates for roots:


`\pm\frac16,\pm\frac13,\pm\frac12`

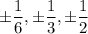
Plugging in each of these will tell you which one is actually a zero. You'll find that both
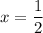
`x=\frac12` and
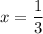
`x=\frac13` both work, which means
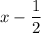
`x-\frac12` and
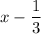
`x-\frac13` are linear factors to the quartic.

To find the remaining factor(s), divide the quartic by the known factors:


`(6x^4+x^3+2x^2-4x+1)/(x-\frac12)=6x^3+4x^2+4x-2`

`(6x^3+4x^2+4x-2)/(x-\frac13)=6x^2+6x+6`

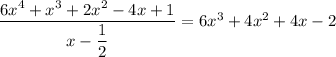
Since
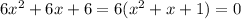
`6x^2+6x+6=6(x^2+x+1)=0` has no real roots, you are left with


`6x^4+x^3+2x^2-4x+1=\left(x-\frac12\right)\left(x-\frac13\right)(6x^2+6x+6)=(2x-1)(3x-1)(x^2+x+1)=0`

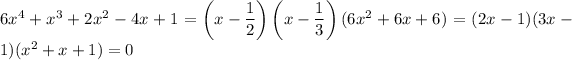
which has two real zeros at
`x=\frac12`,
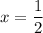
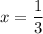
`x=\frac13`. It also has two complex roots at
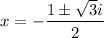
`x=-\frac{1\pm\sqrt3i}2`.