Question

An electric ceiling fan is rotating about a fixed axis with an initial angular velocity magnitude of 0.220 rev/s . The magnitude of the angular acceleration is 0.920 rev/s2 . Both the the angular velocity and angular acceleration are directed counterclockwise. The electric ceiling fan blades form a circle of diameter 0.800 m .

1) Compute the fan's angular velocity magnitude after time 0.208 s has passed.
2)Through how many revolutions has the blade turned in the time interval 0.208 s from Question 1?
3)What is the tangential speed vt of a point on the tip of the blade at time t = 0.208 s ?
4)Calculate the magnitude at of the tangential acceleration of a point on the tip of the blade at time t = 0.208 s .
5)Calculate the magnitude ar of the radial (or centripetal) acceleration of the point at the end of the fan blade.

Answer 1

1) The fan's angular velocity after 0.208 seconds is approximately 2.585 rad/s

2) The number of revolutions the blade has travelled in 0.208 s is approximately 0.066 revolutions

3) The tangential speed of a point on the tip of the blade at time t = 0.208 s is approximately 1.034 m/s

4) The magnitude of the tangential acceleration of a point on the tip of the blade at time t = 0.208 seconds is approximately 2.312 m/s²

Step-by-step explanation:

The given parameters are;

The initial velocity of the fan, n = 0.220 rev/s

The magnitude of the angular acceleration = 0.920 rev/s²

The direction of the angular acceleration and the angular velocity = Clockwise

The diameter of the circle formed by the electric ceiling fan blades, D = 0.800 m

1) The initial angular velocity of the fan, ω₀ = 2·π × n = 2·π × 0.220 rev/s = 1.38230076758 rad/s

The angular acceleration of the fan, α = 2·π×0.920 rad/s² = 5.78053048261 rad/s²

The fan's angular velocity, 'ω', after a time t = 0.208 seconds has passed is given as follows;

ω = ω₀ + α·t

From which we have;

ω = 1.38230076758 rad/s + 5.78053048261 rad/s × 0.208 s = 2.58465110796 rad/s

The fan's angular velocity after 0.208 seconds is ω ≈ 2.585 rad/s

2) The number of revolutions the blade has travelled in the given time interval is given from the angle turned, 'θ', in the given time as follows;

θ = ω₀·t + 1/2·α·t²

θ = 1.38230076758 × 0.208 + 1/2 × 5.78053048261 × 0.208² = 0.41256299505 radians

2·π radians = 1 revolution

∴ 0.41256299505 radians = 0.41256299505 radian× 1 revolution/(2·π radian) = 0.06566144 revolution

The number of revolutions the blade has travelled in 0.208 s ≈ 0.066 revolutions

3) The tangential speed of a point on the tip of the blade at time t = 0.208 s is given as follows;

The tangential speed,
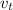`v_t` = ω × r = ω × D/2

At t = 0.208 s, ω = 2.58465110796 rad/s, therefore, we have;

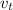`v_t` = ω × D/2 = 2.58465110796 × 0.800/2 = 1.0338604413

The tangential speed,
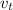`v_t` = 1.0338604413 m/s

The tangential speed ≈ 1.034 m/s

4) The magnitude of the tangential acceleration of a point on the tip of the blade at time t = 0.208 seconds, 'a' is given as follows;

a = α × r = α × D/2

a = 5.78053048261 × 0.800/2 = 2.31221219304

The tangential acceleration, a ≈ 2.312 m/s²