Answer:
Option B is correct
The length of a diagonal of a rectangle is, 6.3 (approx)
Explanation:
Given: The rectangle ABCD with vertices A(-3 , 1) , B(-1 ,3) , C(3,1) and D(1 , -3).
Use Distance formula to calculate the diagonal of Rectangle:
Distance formula for any two points is given by:
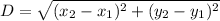
In this rectangle ABCD, the two diagonals are equal in length and bisect each other, i.e, length of BD and length of AC are equal .
therefore, using distance formula to find the length of BD:
here, coordinates are B(-1 , 3) and D(1 ,-3)
then:
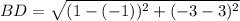 or
or
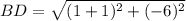
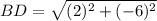 or
or
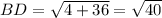
⇒
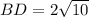 =
=

Therefore, the length of a diagonal of a Rectangle is, 6.3 (approx.)