Question

Express the polynomial as a product of linear factors f(x)=x3-5x2-18x+72

Answer 1

Try out some factors of 72 to see which are roots of f(x).

f(3) = 27 - 45 - 54 + 72 = 0 and f(-3) = -27 - 45 + 54 + 72 = 54,

so 3 is a root and -3 is not. For confirmation, we have f(-4) = 0

and f(6) = 0, so (x - 3)(x + 4)(x - 6)

Answer 2

Answer: The given polynomial can be expressed as (x-3)(x+4)(x-6).

Step-by-step explanation: We are given to express the following cubic polynomial as a product of linear factors :

`f(x)=x^3-5x^2-18x+72.`

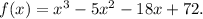
We have the factor theorem that states as follows :

FACTOR THEOREM : If x = a is a zero of the polynomial p(x), then (x - a) is a factor of the polynomial p(x).

If x = 1, then

`f(x)=1^3-5*1^2-18*1+72=1-5-18+72=50\\eq 0.`

If x = 2, then

`f(x)=2^3-5*2^2-18*2+72=8-20-36+72=24\\eq 0.`

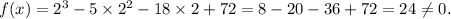
If x = 3, then

`f(x)=3^3-5*3^2-18*3+72=27-45-54+72=0.`

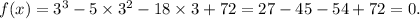
So, x = 3 is a zero of f(x), implies that (x - 3) is a factor of f(x).

Therefore, we have

`f(x)\\\\=x^3-5x^2-18x+72\\\\=x^2(x-3)-2x(x-3)-24(x-3)\\\\=(x-3)(x^2-2x-24)\\\\=(x-3)(x^2-6x+4x-24)\\\\=(x-3)\{x(x-6)+4(x-6)\}\\\\=(x-3)(x+4)(x-6).`

Thus, the given polynomial can be expressed as (x-3)(x+4)(x-6).