Question

An isosceles trapezoid has base angles of 45° and bases of lengths 8 and 14. The area of the trapezoid is

a. 33 sq units
b. 33√2
c. 72 sq units

Answer 1

Area = 0.5 ( sum of two bases ) * height


height = (14- 8)/2 = 3


Area = 0.5 x 3 x (14 + 8 ) = 33 sq units

Answer 2

Option A is correct.

Explanation:

Given an isosceles trapezoid has base angles of 45° and bases of lengths 8 and 14. we have to find the area of isosceles trapezoid.

An isosceles trapezoid has base angles of 45° and bases of lengths 8 and 14.

From the figure attached , we can see an isosceles trapezoid ABCD,

AB = 8cm and CD=14cm

So we have to find the value of AE which is the height of Trapezoid in order to find area.

In ΔAED

`tan\angle 45 =(AE)/(ED)`

⇒
`AE=1* 3`

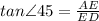
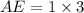
∴ AE = DE =3cm

`\text{The area of the trapezoid=}(h)/(2)* (a+b)`

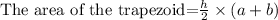
h=3cm, a=14cm, b=8cm

`Area=(3)/(2)*(14+8)=(3)/(2)* 22=33 units^2`

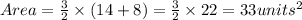
hence,
`\text{The area of the trapezoid is }33 units^2`

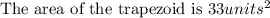
Option A is correct.