Answer:
For x < -3 or 3.438 > 3 the exponential function exceeds the polynomial function.
Explanation:
The given functions are

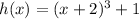
In the given functions f(x) is an exponential function and h(x) is polynomial.
We need to find the x-value in which the exponential function exceeds the polynomial function.
The table of values is shown below,
x f(x) h(x)
-4 1.8×10⁻⁷ -7 f(x)>h(x)
-3 0 0 f(x)=h(x)
-2 4.6×10⁻⁵ 1 f(x)<h(x)
0 0.0012 9 f(x)<h(x)
2 3 65 f(x)<h(x)
3.438 161.845 161.845 f(x)=h(x)
4 768 217 h(x)>f(x)
From the above table it is clear that for x < -3 or 3.438 > 3 the exponential function exceeds the polynomial function.