Question

Use a table of function values to approximate an x-value in which the exponential function exceeds the polynomial function.f(x) = 3(4)^(2x-4)h(x) = (x + 2)^3 + 1

Answer 1

X= 2 I believe my friend

Answer 2

For x < -3 or 3.438 > 3 the exponential function exceeds the polynomial function.

Explanation:

The given functions are

`f(x)=3(4)^(2x-4)`

`h(x)=(x+2)^3+1`

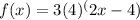
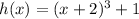
In the given functions f(x) is an exponential function and h(x) is polynomial.

We need to find the x-value in which the exponential function exceeds the polynomial function.

The table of values is shown below,

x f(x) h(x)

-4 1.8×10⁻⁷ -7 f(x)>h(x)

-3 0 0 f(x)=h(x)

-2 4.6×10⁻⁵ 1 f(x)<h(x)

0 0.0012 9 f(x)<h(x)

2 3 65 f(x)<h(x)

3.438 161.845 161.845 f(x)=h(x)

4 768 217 h(x)>f(x)

From the above table it is clear that for x < -3 or 3.438 > 3 the exponential function exceeds the polynomial function.