Question

The height, h, in feet of a flag on one blade of a windmill as a function of time, t, in seconds can be modeled by the equation h=3sin(4pi/5(t-1/2))+12. What is the minimum height of the flag?

Answer 1

9 feet

Explanation:

Answer 2

The minimum height of the flag is 9 feet.

Explanation:

The function representing the height of the flag is given by,

`h(t)=3\sin ((4pi)/(5)(t-(1)/(2)))+12`

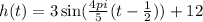
It is required to find the minimum height of the flag.

As, we know,

The function
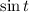`\sin t` have values between [-1,1] for all values of t.

So,
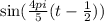`\sin ((4pi)/(5)(t-(1)/(2)))` have values between [-1,1] for all values of t.

Then,
`3\sin ((4pi)/(5)(t-(1)/(2)))` have values between [-3,3] for all values of t.

Thus,
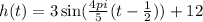`h(t)=3\sin ((4pi)/(5)(t-(1)/(2)))+12` have values between [-3+12,3+12] for all values of t.

That is,
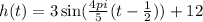`h(t)=3\sin ((4pi)/(5)(t-(1)/(2)))+12` have values between [9,15] for all values of t.

Hence, the minimum height of the flag is 9 feet.