Answer:
The standard deviation of the data is about 6.7.
Explanation:
The given data is
46, 56, 45, 44, 45, 61, 55, 53, 39
Total number of observation is 9.
Formula for mean:
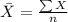
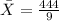
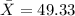
Formula for standard deviation:
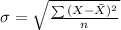
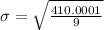
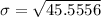
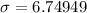
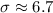
Therefore the standard deviation of the data is about 6.7.