Question

A highway speed monitor is located on the side of the road that has a speed limit of 45 mph. The system records the speeds of passing vehicles. The data below shows the speeds of the first 9 cars that pass. 46 56 45 44 45 61 55 53 39 What is the standard deviation, to the nearest tenth, based on the posted speed limit, 45 mph?

Answer 1

Answer:a0 - 7.2

a1 - mean

a2 - 16.6

Explanation:

I just got answers back on my assignment

Answer 2

The standard deviation of the data is about 6.7.

Explanation:

The given data is

46, 56, 45, 44, 45, 61, 55, 53, 39

Total number of observation is 9.

Formula for mean:

`\bar {X}=(\sum X)/(n)`

`\bar {X}=(444)/(9)`

`\bar {X}=49.33`

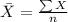
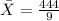
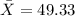
Formula for standard deviation:

`\sigma=\sqrt{\frac{\sum{(X-\bar{X})^2}}{n} }`

`\sigma=\sqrt{(410.0001)/(9)}`

`\sigma=√(45.5556)`

`\sigma=6.74949`

`\sigma \approx 6.7`

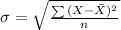
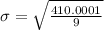
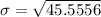
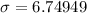
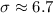
Therefore the standard deviation of the data is about 6.7.