Question

Given that the points (-5, 7), (5, 7), (5, 1), and (-5, 1) are vertices of a rectangle, how much shorter is the width than the length?

A) -5 units
B) -4 units
C) -3 units
D) -2 units
Any improper answers will be reported.
Thanks you.

Answer 1

(-5,7) and (-5,1) is the left side of the rectangle and the width is 7-1 =6
(5,7) and (5,1) is the right side of it. And length will be 5+5 = 10

And difference is 4.

Answer 2

Answer: The correct option is (B) - 4 units.

Step-by-step explanation: Given that the points (-5, 7), (5, 7), (5, 1), and (-5, 1) are vertices of a rectangle.

We are to find the shortness of the width as compared to the length.

Since the adjacent sides of a rectangle makes the length and breadth of the rectangle, so the lengths of two adjacent sides are calculate using distance formula as follows:

the length of the line segment joining the points (-5, 7) and (5, 7) is

`l_1=√((-5-5)^2+(7-7)^2)=√(100+0)=√(100)=10~\textup{units},`

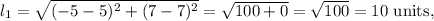
and the length of the line segment joining the points (5, 7) and (5, 1) is

`l_2=√((5-5)^2+(7-1)^2)=√(0+36)=√(36)=6~\textup{units},`

So, the length of the rectangle is 6 units and breadth of the rectangle is 10 units.

Therefore, the width is shorter than the length by

`l_2-l_1=6-10=-4~\textup{units}.`

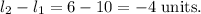
Thus, (B) is the correct option.