Answer:
The cannonball will be at the highest point in 9.375 seconds after the shot.
Explanation:
Suppose we have a quadratic function in the format:
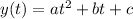
The maximum point will happen when:
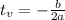
The point will be:

In this problem:

So
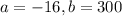
We have to find
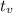
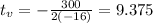
The cannonball will be at the highest point in 9.375 seconds after the shot.